Tutorial 6

Priority Queues

• Queue but first one out is highest priority (lowest key value)
• Each entry:
  • Key: The priority, 0 is the highest priority, 1 is the next
  • Value: The value of the element
• Uses auxiliary comparator to compare keys

Array Implementation

For a sorted list:

• insertion takes $O(n)$, worst case we insert in the end
• RemoveMin is $O(1)$

For an unsorted list:

• insertion is $O(1)$
• removeMin is $o(n)$

Heaps

• Complete binary tree
  • Note to student: consider heap height properties

Heap Order

• The Parent is of higher priority than the child
• key(v) >= key(parent(v))

Last node

• Is the lastmost node of the lowest level

Insert into a Heap

1. Insert at location z, the new last node
2. Restore heap order (up heap)

• keep on swapping with parent until heap order is restored

RemoveMin for a heap

• Swap root node with the last node
• remove the last node (which used to be the root node)
• Restore heap order (perform down heap operation)
  • swap with child nodes (either left or right) until heap order is maintained
  • peformed in $o(\log n)$ time

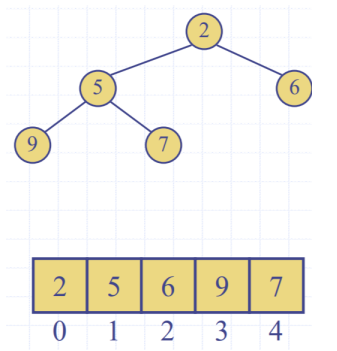
Array Based Heap implementation

• n nodes in an array
• For rank $i$
  • Left child $2i + 2$
  • Right child: $2i + 2$
• Insert: at index n
• Remove: $n-1$

Heap sort

• For $n$ times:
  1. Create a Max Heap
  • Max Heap: Parent priority < Child priority
  2. Swap root (largest number/lowest priority) with last node
  3. Remove last node (the largest number)
  4. Down heap to restore Max Heap Order Performance: $O(n \log n)$ i.e. performing the uphead for $n$ elements $\log n$ times

Heap construction

• For n nodes in a heap (n times)
  1. Insert into a node
  2. Upheap $\log n$

Given two heaps A and B,

1. add a node $k$ as the root
2. Downheap to restore heap order

• $O(n)$ run time